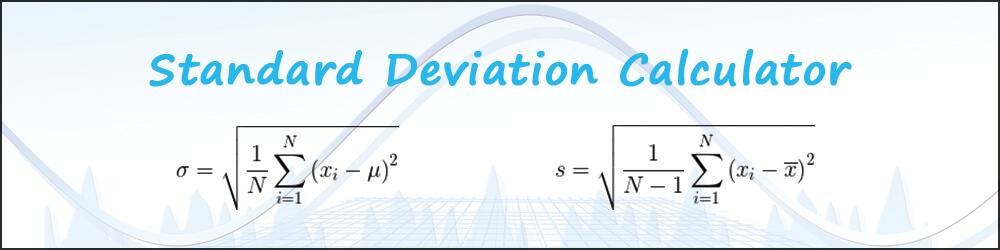
Standard Deviation Calculator

The standard deviation calculator allows you to determine the population and sample standard deviation and variance with mean.

Related Grade Calculator GPA Calculator Z Table T Table

About Standard Deviation Calculator

The standard deviation calculator is a free tool that returns mean, variance, and standard deviation results for a given set of numbers. It runs on pre-defined algorithms and shows the final results quickly and accurately. No need to do the manual calculations and it's free to use.

Mostly, it is used to know whether someone's behavior is normal or extraordinary. In addition, it is used in many fields like finance, business statistics, weather changes, and many more.

For more statistical calculators, check out the Z Score Calculator.

How to Use Standard Deviation Calculator?

It's very easy to operate our calculator. Also, using this you can easily solve any complex problems. Just follow the steps below.

Firstly, enter the numbers or data set in the text box.
Most importantly, the entered values should be space (i.e. 2 3 4 7) or comma (i.e. 2, 3, 4, 7 or 2,3,4,7) seperated.
After entering the values, just click on the "Calculate" button.
As a result, you will get Mean, Population and Sample Variance, and Population and Sample Standard Deviation on your screen.
Lastly, you can reset the calculator using the "Reset" button.

Key Features

User-Friendly Interface

The calculator is useless if the user interface is not so well. That's why we have provided a simple and user-friendly interface to our online users.

Multiple Output

Our tool shows Mean, Variance, and Standard Deviation results. So, it's a one-stop solution to find all the required values.

Fast & Accurate Results

The standard deviation calculator gives fast and 100% accurate results. It works on coded algorithms and is fully tested by our experts.