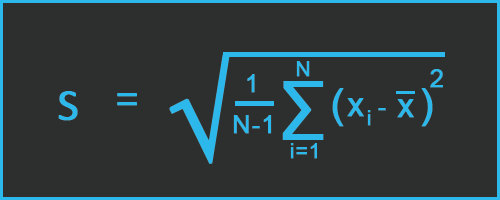How to Calculate Standard Deviation?

For easy understanding, we have divided the whole process into five simple steps.

  1. Calculate the Mean (μ)
  2. Subtract the mean from each data point
  3. Square each difference
  4. Calculate the mean of the square differences
  5. Take the square root of variance

So, let's take an example to understand above all steps one by one.

Example:

Suppose, the data set is: 22, 15, 35, 8, 10. Find out the mean, population variance, and population standard deviation.

Firstly, let's have a look at the population standard deviation formula.

The population standard deviation is equal to the square root of population variance.

Population Standard Deviation Equation

Where,

  • σ = Standard Deviation
  • ∑ = Sum of each
  • Xi = Data points
  • μ = Mean
  • N = Number of data points

Now we are aware of the formula and its components. Let's do the calculation using the five simple steps.

1. Calculate the Mean

Firstly, we need to calculate the mean for a given set of numbers.

The mean is an average of total numbers. It's denoted as "μ" (The greek letter "mu"). Also, it's very easy to calculate the mean.

Just add up all the given data set values and then divide it by a total number of values. Also, if you are dealing with large numbers, you can use the mean calculator to make it easier and faster.

In our case, we have five values. So, we can calculate the mean like this:

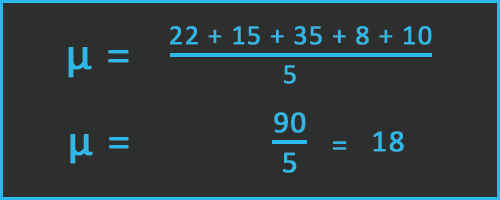
Mean Calculator

So, we get mean (μ) = 18.

Now let's jump to the next step.

2. Subtract the mean from each data points

In this step, we will subtract each data value with mean.

Here we have,

Data values (xi) = 22, 15, 35, 8, 10 and Mean(μ) = 18

So, now we will find (xi - μ).

Subtract the mean from each data points

After subtraction, we get values = 4, -3, 17, -10, -8.

3. Square each difference

In this step, we will square all the values that we got from step 2. So, it will be calculated like this:

  • (4)2 = 16
  • (-3)2 = 9
  • (17)2 = 289
  • (-10)2 = 100
  • (-8)2 = 64

Hence, we get the squared values = 16, 9, 289, 100, 64.

4. Calculate the mean of the squares

In this step, we will find the mean of squared values that we got from step 3.

Also, we will get Variance as a final output from step 4.

Now the question is What is Variance?

Variance is an average of the squared differences from the mean.

Let's see the formula of variance.

Variance Formula

Variance Formula

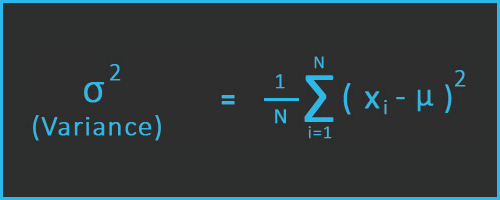
As you can see, we already have found the values of (Xi - μ)2 in step 3. So, our next step is to calculate the variance using these squared values.

For that, we need to calculate the mean of squared values. In short, we need to sum up all the squared values and then divide it with a total number of values. That is 5.

Therefore, the calculation will be:

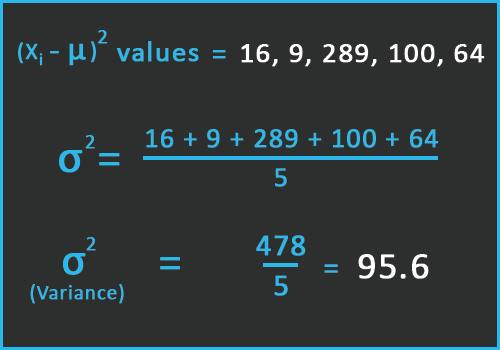
Variance Calculator

So, as a result, we get the population variance = 95.6.

Now, let's go to the final step and find the population standard deviation.

5. Take the square root of variance

In this step, we just need to calculate the square root of variance.

square root of variance

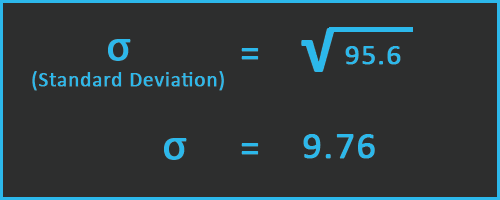
Finally, we get the population standard deviation = 9.76.

Sample Standard Deviation Calculation

In this section, we will discuss the process to find the sample standard deviation.

Firstly, let's have a look at the sample standard deviation formula:

Sample Standard Deviation Formula

As you can see, there is just a small change in this formula as compared to the population standard deviation formula. There is "N-1" rather than "N".

So, step 1, 2, and 3 will remain the same as the population standard deviation calculation when calculating the sample standard deviation.

Only the change will be in step 4 and 5.

Follow the steps below to find the sample standard deviation:

So, we will skip step 1, 2, and 3 and directly jump to the step 4 and 5. That is find out the sample variance using squared values and then find the square root of variance value.

We already have found the squared values: 16, 9, 289, 100, 64.

In population standard deviation, we are dividing the above values with 5. Because the number of values is 5.

But in sample standard deviation, we need to divide the squared total with (N-1) = (5-1) = 4.

After division, we will get the standard variance.

And then we need to calculate the square root of the variance to get the final sample standard deviation.

You can see the step 4 and 5 calculation here:

sample standard deviation result

That's all!

You can easily do the manual calculation by following the five simple steps. But the manual calculation is only for the educational purpose. No need to do it all the time. Because it takes much time and effort to do it. So, it's better to use our standard deviation calculator to make it easier and faster. Also, it gives 100% accurate results.